Физика – наука, которая изучает природу и ее процессы. В ее основе лежат физические величины, которые позволяют нам описать и объяснить различные явления в нашем мире. Однако, не все физические величины одинаковы – они могут быть скалярными или векторными. Скалярные величины имеют только величину, в то время как векторные – и величину, и направление.
Один из примеров векторной величины – скорость. Скорость определяется как изменение положения объекта за единицу времени. Но в чем заключается векторность скорости? Дело в том, что помимо величины, скорость имеет также направление, которое указывает на движение объекта.
Векторная природа скорости становится особенно важной при рассмотрении движения в разных направлениях. Например, разница между движением вперед и движением назад состоит не только в скорости, но и в направлении. Векторная формулировка позволяет нам точно определить и описать, куда движется объект и с какой скоростью.
Векторные физические величины и их объяснение
Векторная физическая величина — это такая физическая величина, которая характеризуется не только числовым значением, но и направлением. То есть для полной характеристики векторной физической величины необходимо знать и ее модуль (числовое значение), и ее направление в пространстве. К примеру, скорость, сила и смещение — все это является векторными физическими величинами.
Вектор в физике представляется графически стрелкой, длина которой представляет модуль вектора, а направление — его направление в пространстве. Векторы могут быть направлены вперед, назад, вверх, вниз или в любом другом возможном направлении.
Почему скорость является векторной физической величиной? Для ответа на этот вопрос рассмотрим пример: два автомобиля с разной скоростью движутся по одной и той же дороге. В данном случае скорость автомобиля необходимо задавать не только величиной, но и направлением — вперед или назад по направлению движения. Это объясняется тем, что движение объекта может быть как в одном, так и в противоположном направлении.
Таким образом, векторная характеристика скорости позволяет определить не только величину скорости, но и направление движения объекта. Без векторной характеристики скорости было бы невозможно полноценно описать движение объекта и предсказать его поведение в пространстве.
Основные понятия векторных величин
Векторные величины играют важную роль в физике, поскольку они позволяют учесть не только величину, но и направление физической величины. Векторные величины имеют следующие основные понятия:
- Модуль: это числовая величина, которая определяет величину физической величины. Модуль вектора всегда является положительным числом или нулем. Например, модуль вектора скорости измеряется в метрах в секунду.
- Направление: это угол или ориентация, которую вектор имеет в пространстве. Направление вектора может быть задано относительно осей координат или в виде угла относительно другого вектора.
- Начало и конец: вектор представляет собой линию с определенным направлением. Начало вектора — это точка, с которой начинается линия, а конец вектора — это точка, на которой заканчивается линия. Они обозначаются буквами A и B соответственно.
- Единичный вектор: это вектор, модуль которого равен 1. Единичные векторы не имеют определенной длины, но всегда указывают в определенном направлении.
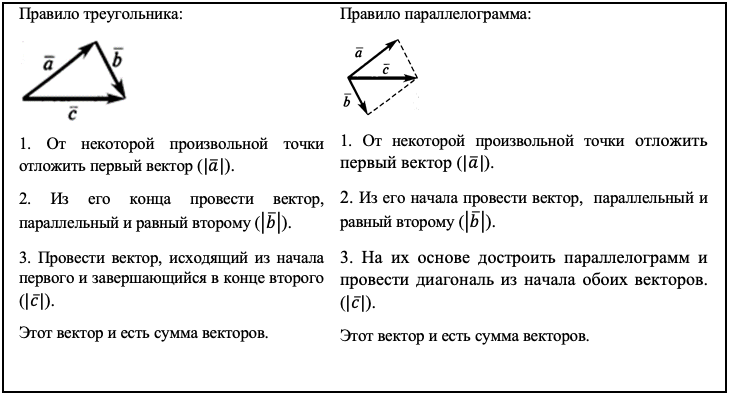
- Сложение векторов: для сложения двух векторов их начала нужно соединить друг с другом и построить новую линию, которая соединяет начало первого вектора с концом второго вектора. Полученная линия является суммой векторов.
Важно отметить, что скорость является векторной величиной, поскольку наряду с ее модулем также имеет значение ее направление. Это позволяет определить, куда и с какой скоростью движется объект.
Определение и примеры
Примером векторной скорости может служить автомобиль, движущийся на дороге. Его скорость будет иметь значение в километрах в час и направление, указывающее, куда движется автомобиль. Если автомобиль движется на север, то его скорость будет иметь направление севера.
Другим примером является воздушный шар, поднимающийся вверх. Его скорость также будет векторной величиной, с направлением вверх.
Из этих примеров видно, что скорость не может быть полностью определена только численным значением. Векторная характеристика позволяет учесть направление движения, что делает ее более полной и точной для описания физических явлений.
| Объект | Численное значение скорости | Направление движения |
|---|---|---|
| Автомобиль | 60 км/ч | На север |
| Воздушный шар | 10 м/с | Вверх |
Сложение векторов
Первый метод – это графическое сложение векторов. Для этого нужно нарисовать векторы в соответствующем масштабе на плоскости и измерить длины каждого вектора. Затем нужно положить начало второго вектора на конец первого и провести прямую от начала первого вектора до конца второго. Точка пересечения этой прямой с осью координат будет являться концом результирующего вектора.
Второй метод – это аналитическое сложение векторов. Для этого нужно знать координаты начальных и конечных точек векторов. Для сложения можно просто сложить соответствующие координаты: сложить x-координаты и y-координаты, чтобы получить результат.
Третий метод – это метод треугольников. Для этого нужно провести прямую от начала первого вектора до конца второго и от начала второго вектора до конца первого. В результате получатся два треугольника. Используя теорему косинусов, можно найти все стороны и углы этих треугольников и определить длину и направление результирующего вектора.
Сложение векторов – это важная операция, которая позволяет находить общий результат движения нескольких тел или изменение скорости и направления движения. Именно поэтому скорость является векторной величиной, так как она учитывает как модуль, так и направление движения.
Умножение вектора на скаляр
Умножение вектора на скаляр осуществляется путем умножения каждой компоненты вектора на скаляр по отдельности. Например, если имеется вектор В = (2, 4, 6) и скаляр а = 3, то результатом умножения будет новый вектор С = (2*3, 4*3, 6*3) = (6, 12, 18).
Умножение вектора на скаляр имеет несколько свойств:
| 1. Умножение вектора на 1 дает вектор, равный исходному. |
| 2. Умножение вектора на 0 дает нулевой вектор, у которого все компоненты равны 0. |
| 3. Умножение вектора на отрицательный скаляр изменяет его направление на противоположное, но сохраняет его длину. |
| 4. Умножение вектора на положительный скаляр увеличивает его длину в соответствии с модулем скаляра. |
Умножение вектора на скаляр широко применяется во многих областях науки и техники. Например, в физике, при вычислении силы, действующей на тело, умножение вектора силы на число позволяет определить величину силы при заданных условиях.
Почему скорость является векторной
В отличие от скалярных величин, которые полностью характеризуются числовыми значениями и не имеют направления, векторные величины имеют и численную характеристику, и определенное направление в пространстве. Скорость, как векторная величина, не только указывает на величину движения, но и позволяет определить направление, в котором происходит движение.
Направление скорости может быть абсолютным или относительным, в зависимости от выбранной системы отсчета. Абсолютное направление скорости задается относительно фиксированной точки, такой как Север или Восток, в то время как относительное направление скорости определяется относительно другого тела или объекта. Например, движение автомобиля может быть описано как движение на восток со скоростью 50 км/ч, относительно земной поверхности, или как движение на юг со скоростью 20 км/ч, относительно другого автомобиля.
Векторная характеристика скорости дает возможность проводить различные операции над скоростными векторами, такие как сложение и вычитание. При сложении скоростей учитываются их значения и направления, что позволяет определить итоговое значение скорости после сложения. Например, если два объекта движутся в одном направлении, то их скорости складываются, а если два объекта движутся в противоположных направлениях, то их скорости вычитаются.
Таким образом, скорость является векторной величиной, так как содержит информацию не только о числовом значении движения, но и о его направлении в пространстве. Это позволяет более полно и точно описывать движение объектов в физике.
Скорость как физическая величина
Скорость является векторной величиной, так как она имеет не только числовое значение, но и направление. Для полного описания скорости необходимо указать как модуль скорости (величину изменения пути за единицу времени), так и его направление.
Вектор скорости указывает на то, в каком направлении и с какой интенсивностью движется объект. Направление может быть как положительным, так и отрицательным, в зависимости от выбранной системы отсчета. Например, при движении автомобиля по прямой вперед его скорость будет положительной, а при движении назад — отрицательной. Таким образом, вектор скорости позволяет учесть не только числовые значения, но и ориентацию движения.
Скорость имеет физическую размерность, которая обозначается в Международной системе единиц (СИ) как метры в секунду (м/с). Для измерения скорости используются различные приборы, такие как спидометры в автомобилях или специальные датчики в спортивных соревнованиях.
Векторная природа скорости позволяет учесть все особенности движения объектов, такие как их направление, изменение скорости или то, что объект может двигаться с разной скоростью в разные моменты времени. Поэтому понимание скорости как векторной величины является важным для точного описания и анализа движения в физике.
Вопрос-ответ:
Что такое векторные физические величины?
Векторные физические величины — это величины, которые описываются не только числовым значением, но и направлением. Такие величины имеют не только модуль (величину), но и ориентацию в пространстве.
Какие примеры векторных физических величин существуют?
Примерами векторных физических величин являются скорость, ускорение, сила, момент силы, импульс и др.
Почему скорость является векторной величиной?
Скорость является векторной величиной, потому что она имеет не только числовое значение (модуль), но и направление. Направление скорости указывает на то, в какую сторону движется тело.
Зачем нужно учитывать направление скорости?
Учет направления скорости важен для полного описания движения тела. Например, два тела с одинаковой скоростью, но движущиеся в противоположных направлениях, будут иметь различное движение и поведение в пространстве.